Pasa Analytics | Solutions d'Analyse Avancée

1. Bases de l'adsorption et transport réactif [septembre 2024]

Méthodologie

Cette étude s'appuie sur la résolution numérique de l'équation d'advection-diffusion-réaction par différences finies et éléments finis (Python/FEniCS).

Équation fondamentale du transport avec adsorption

Le transport d'un contaminant dans un milieu poreux (filtre) est régi par l'équation :

∂c_L/∂t = -μ ∂c_L/∂x + D ∂²c_L/∂x² + γ

où le terme source γ représente l'adsorption/désorption sur le substrat du filtre :

γ = -K_d ρ_s (1-θ)/θ · ∂c_L/∂t

avec :

θ : porosité du filtre
ρ_s : masse volumique du filtre
K_d : coefficient de partage (adsorption)

Mise à l'échelle et facteur de retard

L'équation peut se réécrire sous forme d'une équation d'advection-diffusion classique avec des coefficients effectifs :

∂c_L/∂t = -u* ∂c_L/∂x + D* ∂²c_L/∂x²

u* = u / R

D* = D / R

R = 1 + K_d ρ_s (1-θ)/θ

Le facteur de retard R > 1 traduit le ralentissement du front de concentration dû à l'adsorption : plus R est élevé, plus le filtre retient efficacement le contaminant.

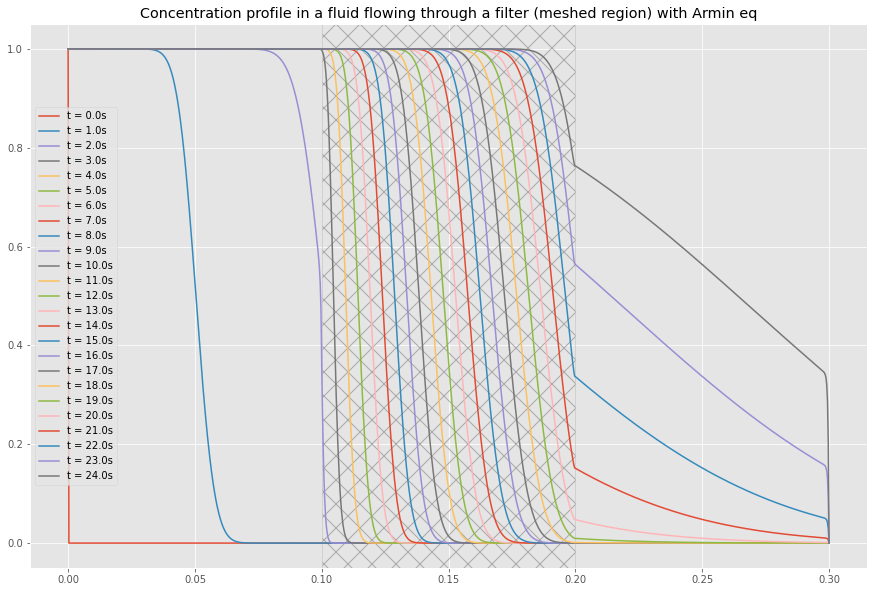
Profils temporels de Concentration avec un facteur de retard R = 10.4.

Profil de concentration dans le filtre - Solution numérique de l'équation d'advection-diffusion-réaction

Modèle complet d'adsorption-diffusion

Le système complet s'écrit, en considérant les concentrations dans le fluide (c_ℓ) et dans le filtre (c_f) :

∂c_ℓ/∂t = D_ℓ ∆c_ℓ + κ ∆c_f - α u c_ℓ - u·∇c_ℓ

∂c_f/∂t = D_f ∆c_f + α u c_ℓ - κ ∆c_f

∂α/∂t = ε c_f

Ce modèle intègre :

α : coefficient d'adsorption du contaminant sur le filtre
κ : coefficient de diffusion du filtre vers le fluide (désorption)
ε : facteur de saturation (dépendance de l'adsorption au chargement du filtre)

Profils temporels de Concentration avec un coefficient d

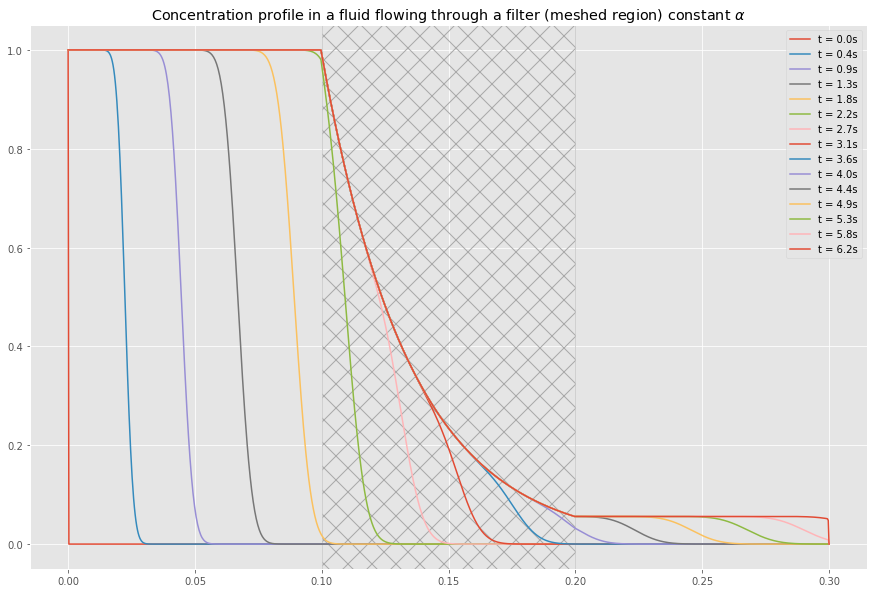
Évolution temporelle de la concentration adsorbée sur le substrat du filtre

Cas particulier : coefficient d'adsorption variable

Lorsque le filtre se charge, l'efficacité d'adsorption diminue. On modélise ce phénomène par :

α(t) = α₀ · (1 - ε · c_f)

Cette non-linéarité conduit à une saturation progressive du filtre et à une percée (breakthrough) du contaminant.

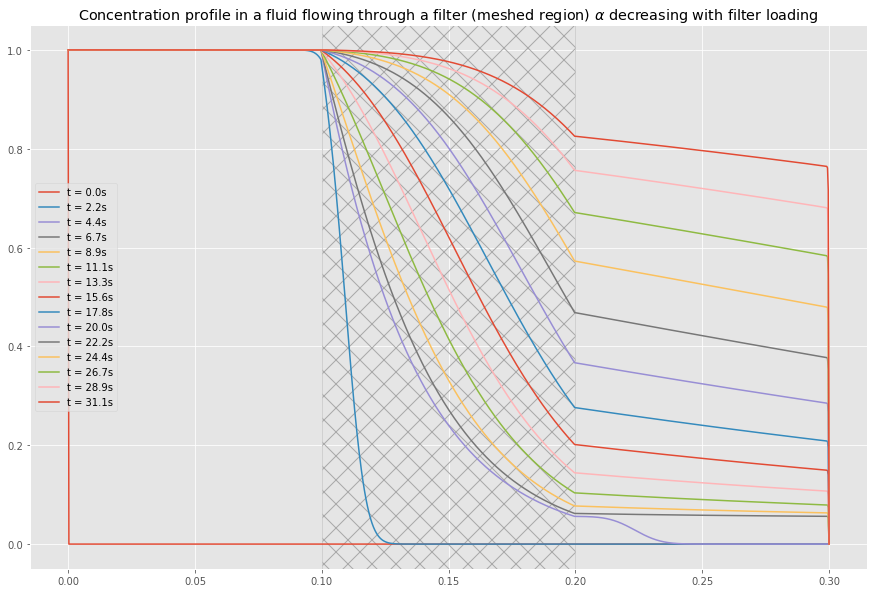
Modèle non-linéaire : décroissance du coefficient d'adsorption avec le chargement du filtre. La concentration de sortie augmente.

Interprétation physique

Facteur de retard R : quantifie le ralentissement du contaminant dans le filtre
Efficacité initiale : proche de 100% tant que c_f ≪ capacité maximale
Percée : apparition du contaminant en sortie lorsque le filtre sature
Modèle de Langmuir : extension possible avec isotherme d'adsorption non-linéaire

2. Migration de contaminants depuis un tube [novembre 2024]

Cette section présente la simulation de la migration de substances depuis la paroi d'un tube polymère vers un fluide en écoulement.

Configuration géométrique

Diamètre interne : 4 mm
Épaisseur de paroi : 0.6 mm
Longueur : 1 m
Débit : 100 mL/h
Volume interne : 12.57 mL

Propriétés des substances

Deux substances aux diffusivités contrastées sont simulées :

Paramètres de migration

Substance 1 : Dₛ = 10⁻⁶ mm²/s, Dℓ = 5×10⁻⁴ mm²/s, μ = 72 μg/g
Substance 2 : Dₛ = 5×10⁻⁶ mm²/s, Dℓ = 2×10⁻³ mm²/s, μ = 252 μg/g
Coefficient de partage : F = 10 (concentration dans solide / concentration dans fluide à l'équilibre)

Régime de diffusion pure

En l'absence d'écoulement, la migration est régie par la seconde loi de Fick :

∂c/∂t = ∇·(D∇c)

Après 1 heure de diffusion, les concentrations dans le fluide atteignent :

Substance 1 : 0.0408 mg dans le volume interne (12.57 mL)
Substance 2 : 0.2420 mg

Concentration par diffusion pure après 1h.

Migration par diffusion pure : profil de concentration après 1 heure.

Régime d'advection-diffusion

Avec écoulement, l'équation de transport devient :

∂c/∂t = ∇·(D∇c) - v·∇c

où le profil de vitesse v est solution des équations de Navier-Stokes :

∂v/∂t + v·∇v = ∇·(ν∇v) - g - (1/ρ)∇p

Pour un débit de 100 mL/h (vitesse débitante ≈ 2.21 mm/s), le nombre de Reynolds est très faible (Re ≪ 1), le régime est laminaire avec un profil parabolique (Poiseuille).

Concentration par diffusion-advection après 1h.

Migration avec écoulement : profil de concentration à t = 2 heures

Résultats pour un écoulement continu

Pour un volume total écoulé de 400 mL (durée : 4 heures), les masses cumulées de contaminants sont :

0.125 mg

Substance 1

1.044 mg

Substance 2

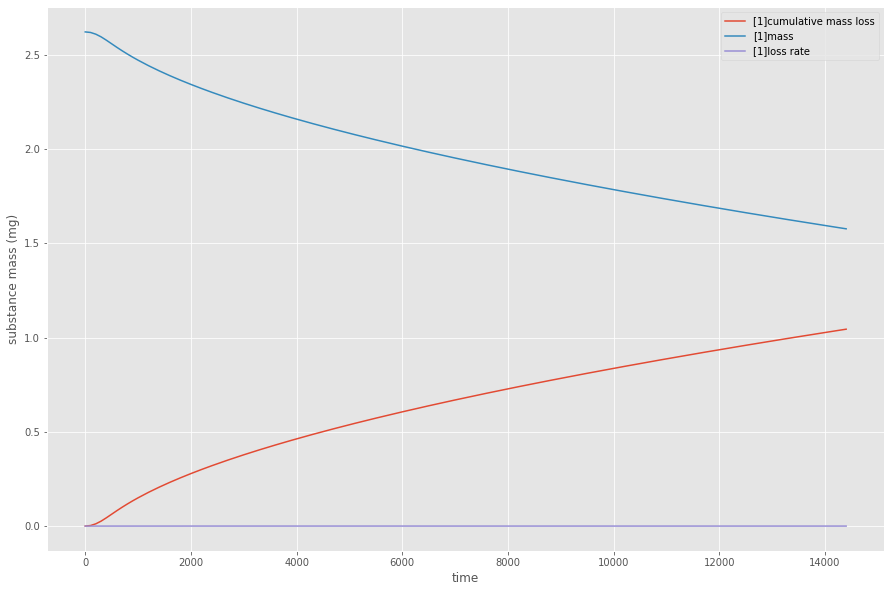
Masse cumulée de contaminants dans le fluide en fonction du volume écoulé

Impact du profil de débit

Trois scénarios sont comparés pour un même volume total (400 mL) :

Scénario A - Continu

Débit constant 100 mL/h

m₁ = 0.125 mg
m₂ = 1.044 mg

Durée: 4h00

Scénario B - Interrompu

100 mL/h (1.5h) → arrêt 1h → reprise

m₁ = 0.140 mg (+12%)
m₂ = 1.150 mg (+10%)

Durée: 5h00

Scénario C - Ralenti

100 mL/h (1.5h) → arrêt 1h → 50 mL/h

m₁ = 0.176 mg (+41%)
m₂ = 1.427 mg (+37%)

Durée: 7h30

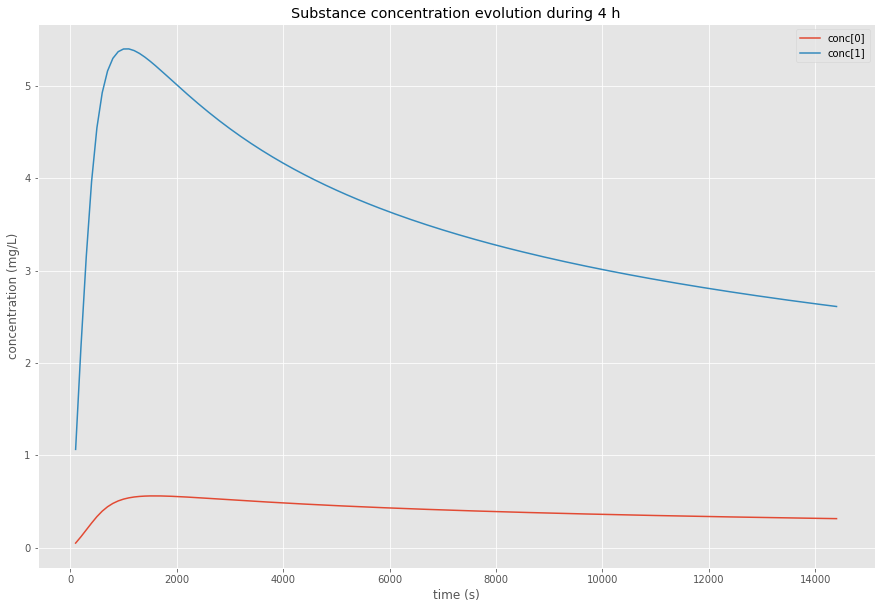
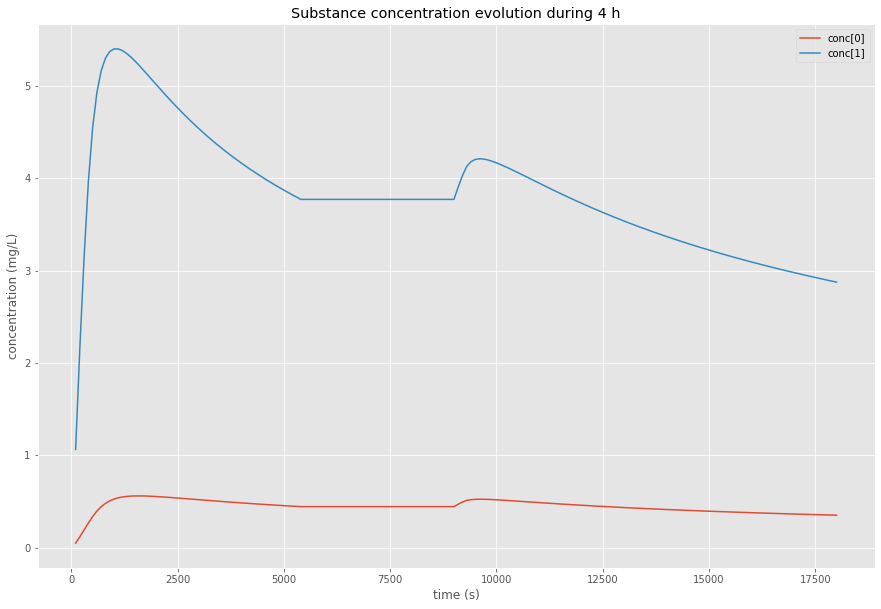
Flux interrompu et réduction de vitesse.

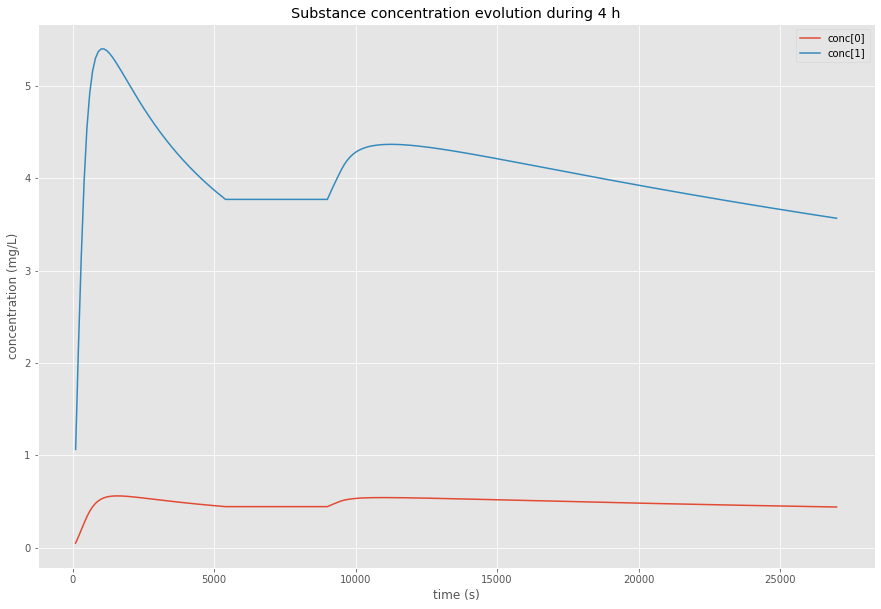
Trois scénarios de débit : continu, interrompu, interrompu avec réduction de vitesse

Interprétation : Les interruptions et ralentissements augmentent significativement la migration car le temps de contact entre le fluide et la paroi du tube est prolongé. Un procédé continu minimise la contamination.

3. Modélisation avancée d'un système de filtration [décembre 2024]

Régime stationnaire et loi de Beer-Lambert

Dans le cas stationnaire, en négligeant la diffusion depuis le filtre (κ ≈ 0), le système se réduit à :

0 = -α u c_ℓ - u ∂c_ℓ/∂x

dont la solution est une exponentielle décroissante :

c_ℓ(x) = c₀·exp(-α x)

Cette relation, analogue à la loi de Beer-Lambert en absorption optique, caractérise l'atténuation du contaminant dans le filtre.

Décroissance exponentielle de la concentration dans le filtre (zone hachurée) pour une adsorption constante.

Courbe de percée (breakthrough curve)

La grandeur clé pour dimensionner un filtre est la courbe de percée : évolution de la concentration en sortie en fonction du temps ou du volume traité.

[Simulation] Courbe de percée (breakthrough)

Concentration en sortie de filtre vs temps

Évolution de la concentration en sortie de filtre - saturation progressive du média filtrant

Paramètres optimaux de filtration

L'optimisation d'un système de filtration repose sur le compromis entre :

Efficacité : capacité à retenir les contaminants (α élevé, R élevé)
Durée de vie : volume traité avant percée (capacité du filtre)
Pertes de charge : impact sur le débit (équations de Navier-Stokes en milieu poreux, loi de Darcy)

ΔP = (μ·Q·L)/(K·A) (loi de Darcy)

avec K la perméabilité du milieu poreux (m²), fonction de la porosité et de la taille des pores.

4. Système couplé : tube + filtre [décembre 2024]

Le modèle complet intègre :

Migration : diffusion depuis les parois du tube + advection par l'écoulement
Filtration : adsorption du contaminant sur le média filtrant
Couplage : la concentration en entrée du filtre est la concentration en sortie du tube

[Simulation] Système couplé : tube + filtre

Tube (migration)

Filtre (adsorption)

Concentration entrée: 0.125 mg/L · Efficacité filtration: 92%

Modèle complet : migration depuis les parois du tube suivie d'une filtration

Étude de cas

Considérons un système où :

Le fluide traverse un tube de 1 m (migration depuis la paroi)
Puis un filtre de 10 cm d'épaisseur (adsorption)
Débit : 100 mL/h
Substance 1 (paramètres précédents)

Résultats de simulation

Concentration entrée tube

0 μg/L

Concentration sortie tube

125 μg/L

Concentration sortie filtre

10 μg/L

Efficacité globale de rétention : 92%

Analyse de sensibilité

L'efficacité du système couplé dépend de plusieurs paramètres :

Paramètre : Épaisseur filtre

5 cm → 85% 10 cm → 92% 15 cm → 96%

Loi exponentielle

Paramètre : Débit

50 mL/h → 95% 100 mL/h → 92% 200 mL/h → 86%

Temps de contact

Paramètre : Migration tube

Substance 1 → 92% Substance 2 → 78%

Dépendance à la diffusivité

[Simulation] Comparaison des scénarios

Continu

Interrompu

Ralenti

Masse migrée: +12% (interruption), +41% (ralentissement)

Impact du profil de débit sur la masse totale de contaminants migrés

Conclusion et perspectives

La simulation numérique des phénomènes couplés de migration et filtration permet de :

Quantifier la contamination réelle d'un produit en fonction des paramètres procédés
Optimiser le dimensionnement du système de filtration (épaisseur, porosité, débit)
Anticiper la saturation du filtre et planifier son remplacement
Comparer différents scénarios de production (continu vs discontinu)

Applications industrielles :

Pharmaceutique : purification de principes actifs, contrôle des extractables et relargables
Agroalimentaire : filtration des boissons, validation des matériaux d'emballage
Environnement : traitement des eaux, barrières réactives perméables
Chimie : séparation et purification en continu

Développement sur mesure de modèles de filtration adaptés à votre procédé