1. Fil quantique
Introduction
Cette étude a pour objectif le calcul du spectre d'absorption lumineuse de fils quantiques d'arséniure de gallium-aluminium (AlxGa1-xAs) fabriqués en laboratoire.
Les hétérostructures sont obtenues par variation contrôlée de la composition en aluminium durant la croissance. La microscopie électronique révèle des renflements riches en Al qui forment le confinement quantique.
Microscopie électronique d'un fil quantique AlGaAs
Le calcul de l'absorption nécessite la détermination préalable des états électroniques et des états de trous, qui se localisent dans les régions de plus bas potentiel. Ces états permettent les transitions optiques avec émission ou absorption de photons.
Une absorption négative indique une amplification de la lumière, propriété exploitée dans les milieux amplificateurs des lasers.
Calcul des états électroniques
La résolution de l'équation de Schrödinger pour cette géométrie complexe est effectuée par séparation des variables : partie périodique le long du fil, partie transverse résolue par éléments finis après maillage.
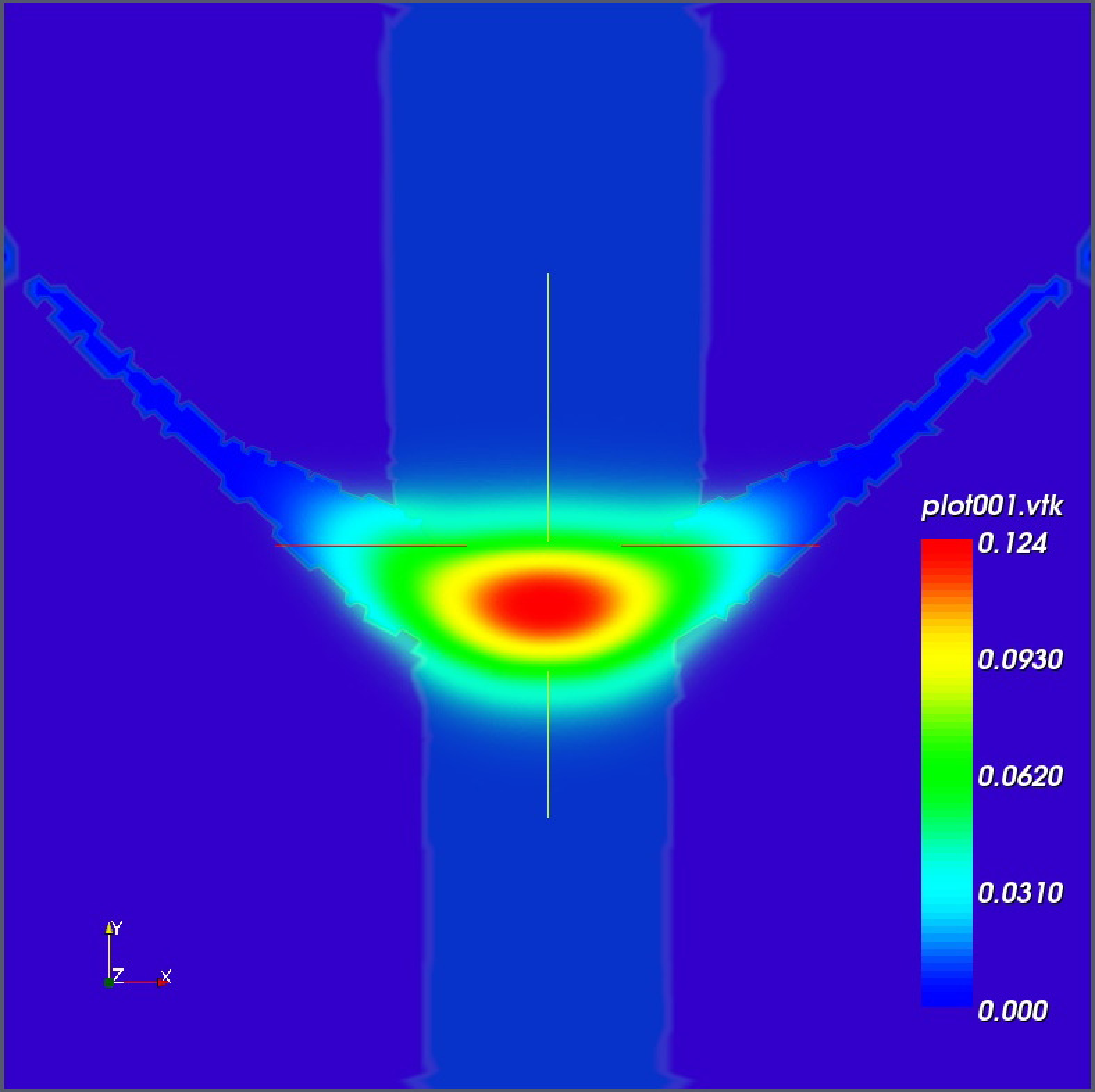
État fondamental
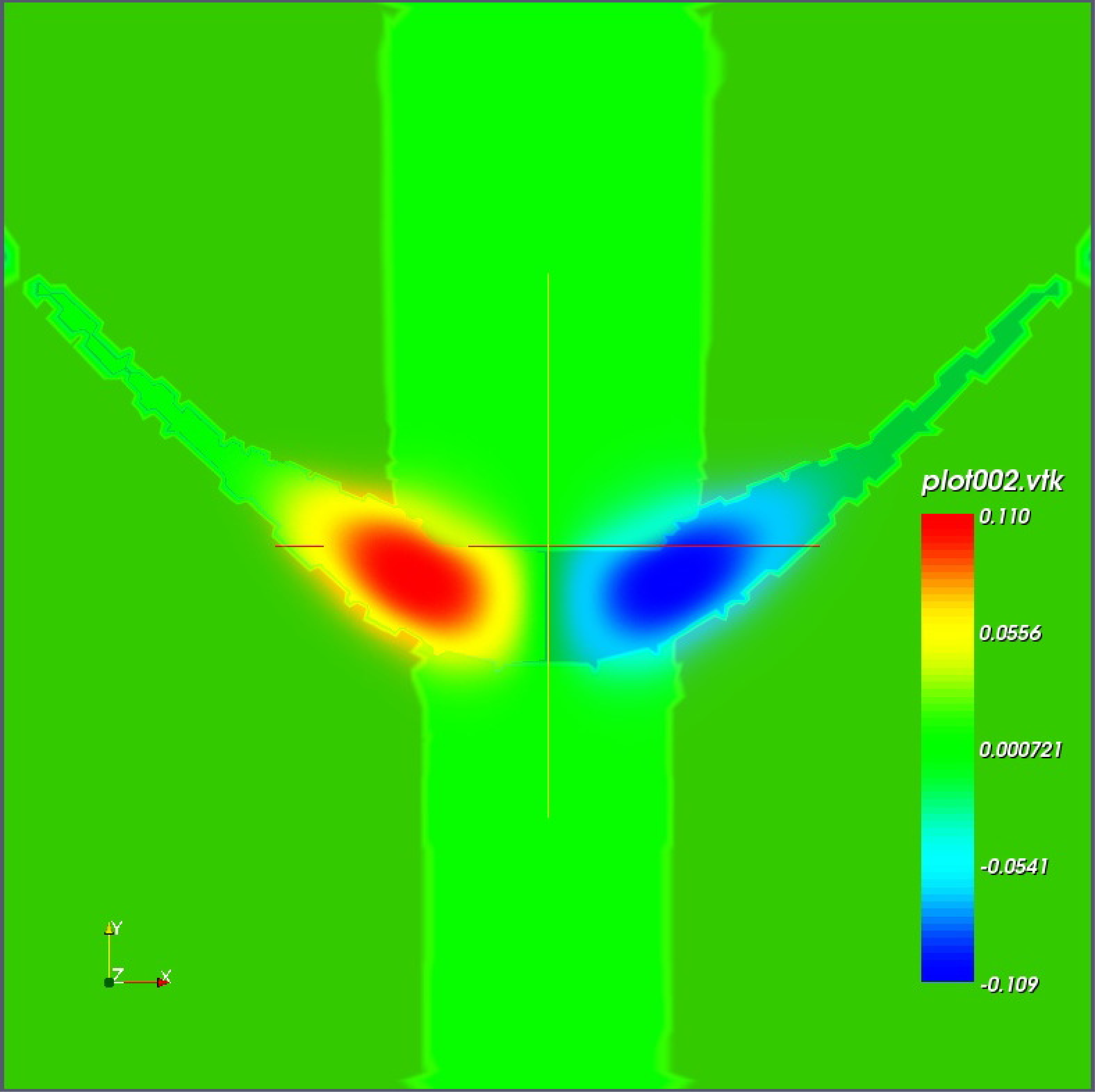
1er état excité

2ème état excité
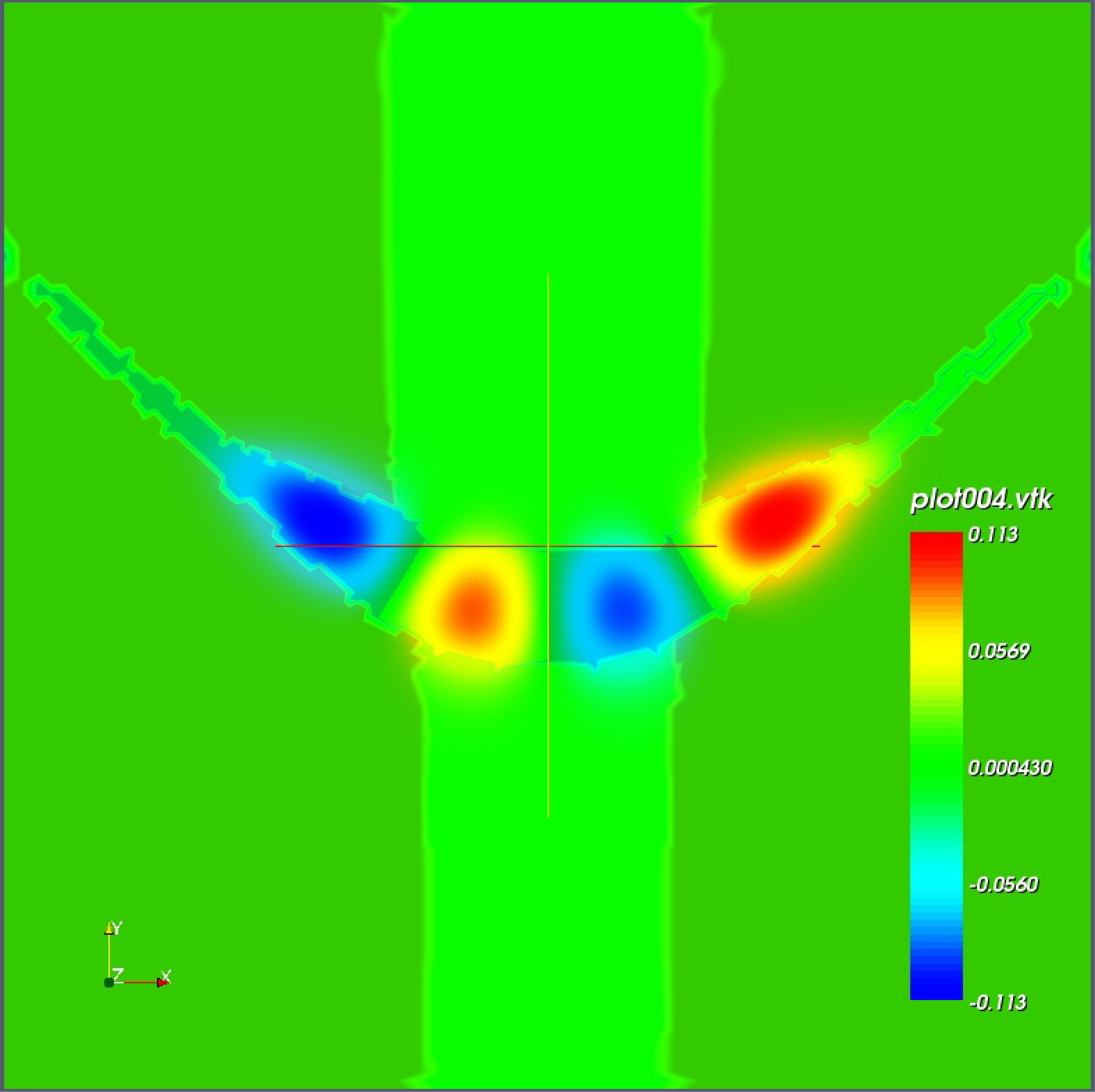
3ème état excité
Densités de probabilité des 4 premiers états électroniques
Les états présentent une localisation caractéristique dans la région de confinement, avec des énergies discrètes typiques des systèmes quantiques confinés.
Traitement des états de trous
Contrairement aux électrons, les trous dans les semi-conducteurs nécessitent un traitement spinoriel complet. Le hamiltonien de Luttinger-Kohn, tenant compte du mélange des bandes de valence (j=3/2), remplace l'approximation de masse effective simple.

Sans mélange de bandes de valence
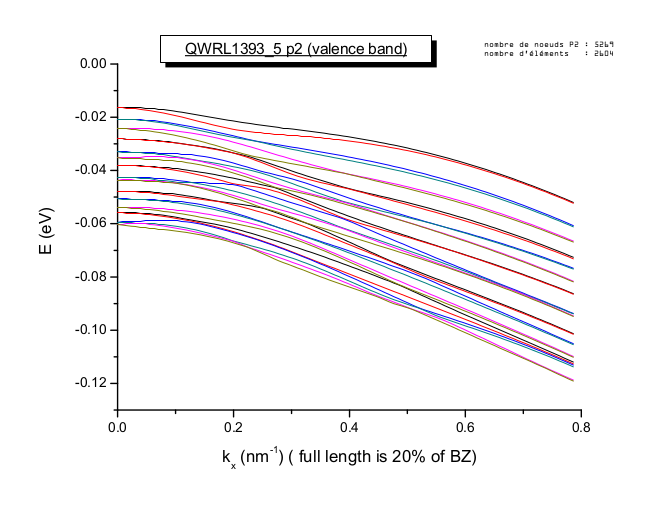
Avec mélange de bandes de valence
Comparaison des dispersions énergétiques avec et sans mélange de bandes
Le mélange des bandes lève les dégénérescences et modifie significativement la structure de bande des trous, avec des implications importantes pour les transitions optiques.
Calcul des spectres d'absorption
Les amplitudes de transition sont calculées à partir des fonctions d'onde électroniques et de trous, incluant les effets de polarisation lumineuse et les peuplements statistiques des niveaux.
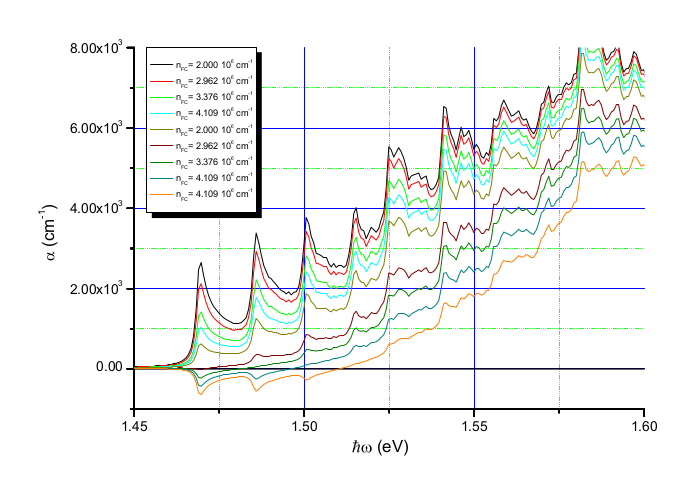
Résolution grossière
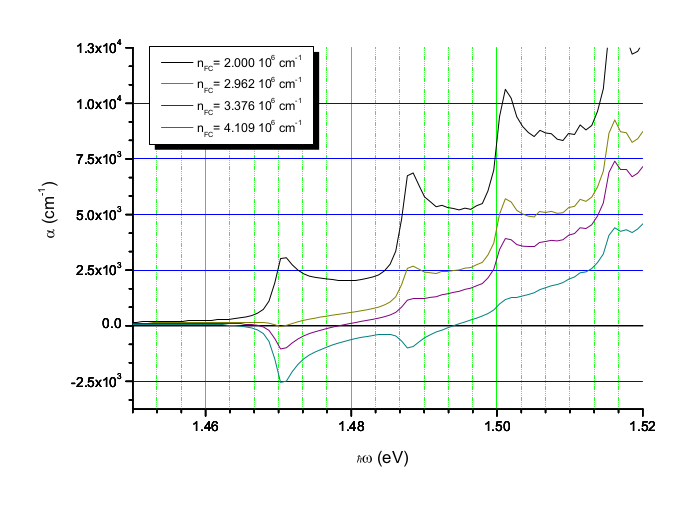
Résolution fine
Spectres d'absorption pour différentes résolutions de calcul
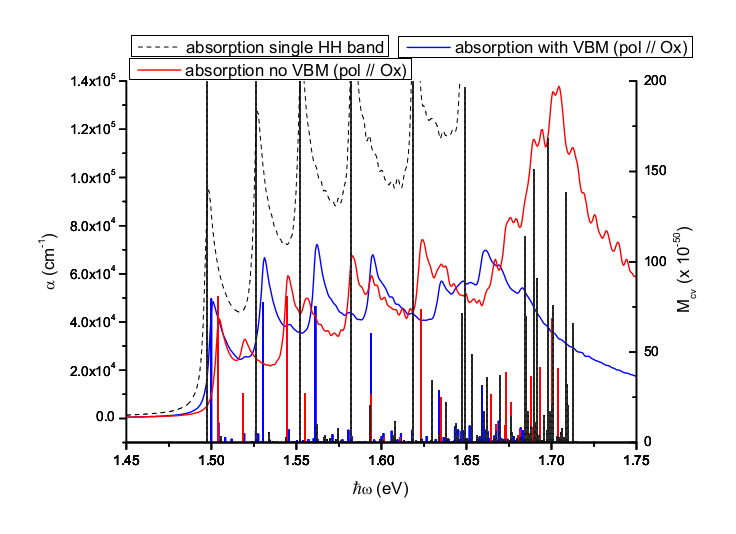
Comparaison des spectres d'absorption pour différentes polarisations
Note technique
Les calculs incluent : traitement correct des fonctions d'enveloppe, couplage lumière-matière dipolaire électrique, et distribution de Fermi-Dirac pour les peuplements.
2. Boîte quantique
Les boîtes quantiques, ou points quantiques, sont des nanostructures semiconductrices offrant un confinement tridimensionnel des porteurs de charge.
Modèle théorique sphérique
Pour cette étude, nous avons développé un modèle théorique de boîtes quantiques sphériques avec les paramètres :
- Potentiels de confinement pour électrons et trous
- Rayon effectif de la boîte
- Paramètres de matériau (masses effectives, constantes diélectriques)
- Effets de taille quantique
États à plusieurs particules
L'originalité de cette étude réside dans l'exploration systématique des états corrélés à N corps :
Excitons (X)
États liés électron-trou
eh
Trions
Deux électrons + un trou ou deux trous + un électron
eeh / ehh
Bi-excitons (XX)
États liés à deux paires électron-trou
eehh
Ces états composites présentent des énergies de liaison et des propriétés optiques distinctes de la simple somme des particules individuelles.
Approche méthodologique
Résolution de l'équation de Schrödinger multiparticulaire par méthode de configuration interaction, avec fonctions de base Bessel sphériques.