1. Résistance mécanique[janvier 2024]
Cette étude fut réalisée en R.
L'analyse de données bayesienne ne donne pas des résultats uniques, ponctuels, mais des intervalles de valeurs probables. En ce sens, cette méthode est honnête et ne promet pas plus que ce qui se trouve dans les données. Si une mesure expérimentale, une enquête, un sondage recueille des données concernant un sujet d'étude, plusieurs biais peuvent être inhérents à la méthode de collection. Partant d'un modèle d'experts, l'analyse bayesienne, via une étude des chaînes de causalités, est la méthode idéale qui permet d'obtenir les meilleures prédictions (inférences) possibles, sur la base des données récoltées, sans utiliser d'hypothèses cachées. Le résultat est alors une distribution de probabilité (qui indique pour chaque valeur possible de la solution, le degré de vraisemblance extrait des données). Cette information est bien plus riche et complète (honnête même), qu'une valeur unique (la solution), qui sous-entend un degré de précision infini (et qui n'est pas réaliste). L'avantage de la méthode bayesienne, par rapport aux autres méthodes d'analyse des données, est qu'elle manipule naturellement les distributions de probabilité et permet d'obtenir des inférences directement à partir des solutions obtenues, inférences qui sont également des distributions et que l'on peut directement comparer aux mesures réelles.
L'objectif de cette étude exploratoire était de déterminer les moyens et la possibilité de paramétrer la résistance mécanique Rp\(_{0.2}\) d'un métal.
Plus particulièrement, ce qui nous intéressait était la courbe de vieillissement de la résistance du métal (qui devient plus rigide avec le temps). Les données
empiriques sont du types illustrés dans la figure suivante (ces données sont simulées)
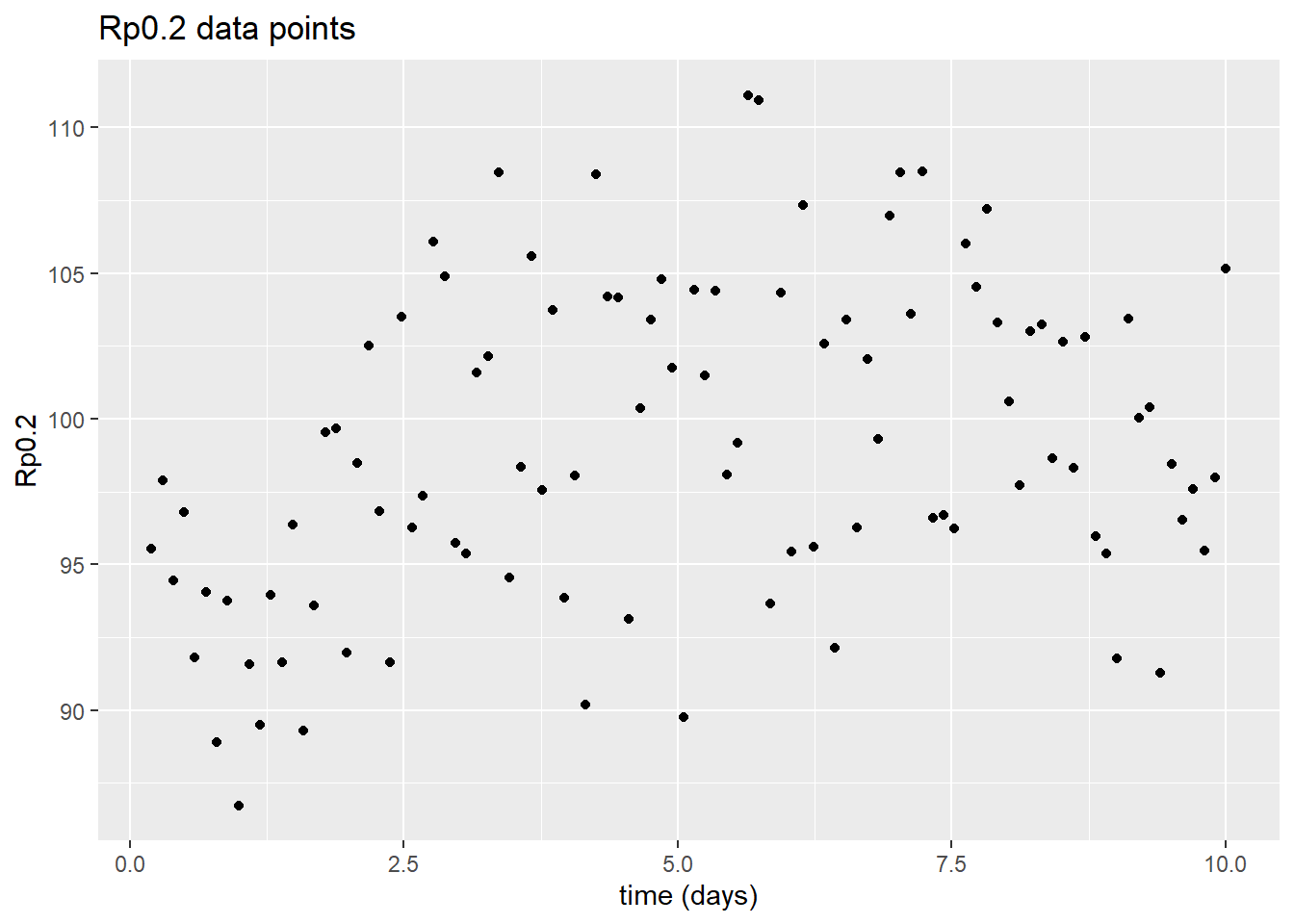
L'analyse bayesienne est particulièrement bien adaptée pour la détermination de ces paramètres (bien que ce soit un problème linéaire simple et que d'autres méthodes équivalentes existent pour déterminer ces paramètres) en conservant une maîtrise des valeurs de dispersion, due au bruit des mesures (on veut savoir quelle dispersion dans la valeur des paramétres est compatible avec les valeurs expérimentales: on ne veut pas postuler une précision plus grande que ne le permet la mesure).
Ainsi, avec un premier ensemble de mesures (qui sont ici simulées) montrées dans le graphe suivant
on obtient le résultat (la ligne sombre et la zone rouge) de la détermination des paramètres

La zone rose montre l'intervalle de confiance \(95 \% \) des valeurs simulées à partir de la solution. Cet intervalle peut alors être comparé avev les valeurs expérimentales.
2. Deux alliages[janvier 2024]
Le pas suivant dans l'étude était la détermination des paramètres pour deux alliages différents
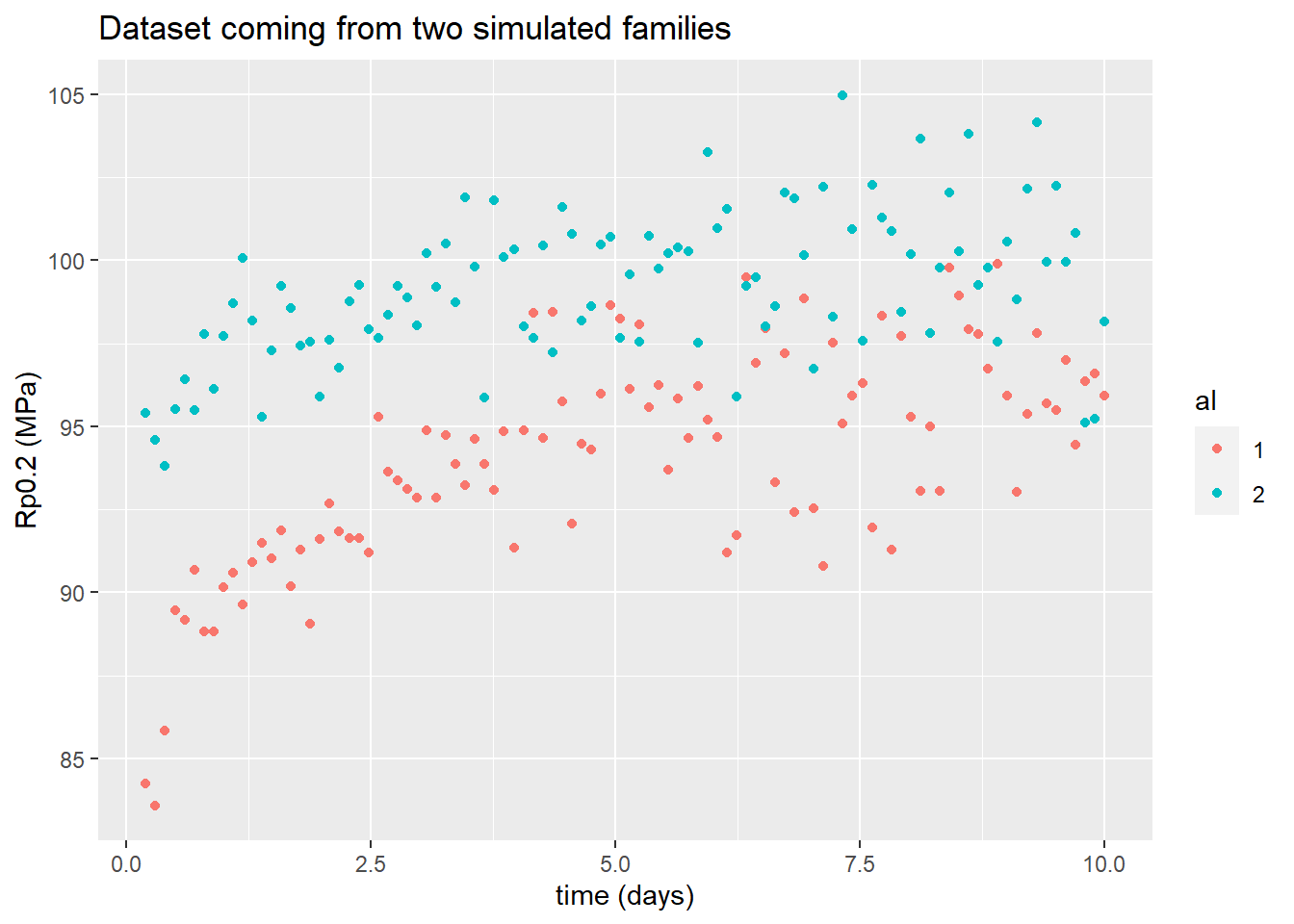
Pour trouver la solution dans cette situation il faut conditionner les paramètres à l'alliage. Le résultat est illustrés ci-dessous
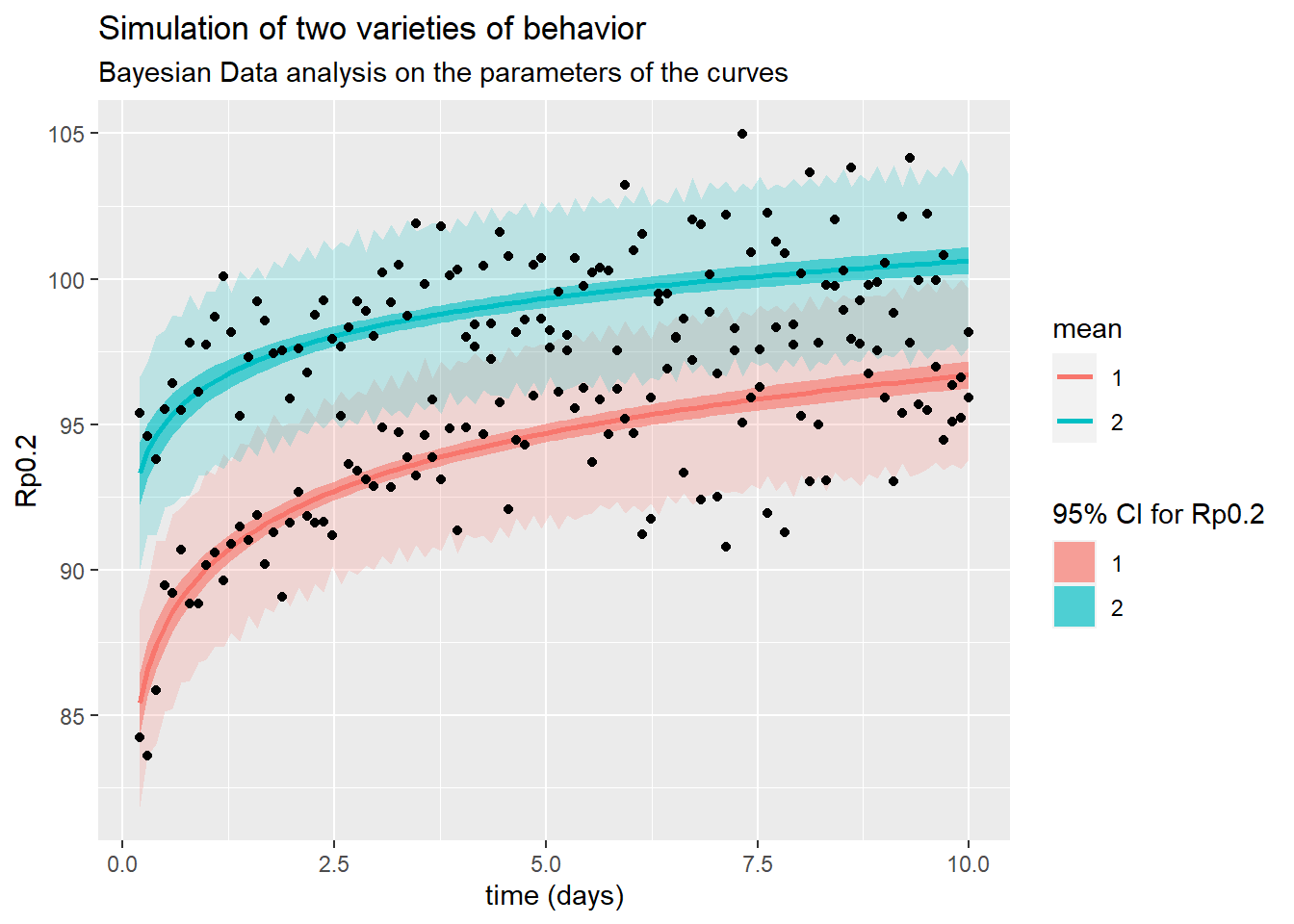
3. Dépendance dans la composition[janvier 2024]
Enfin, la dernière étape a consisté à conditionner les paramètres aux concentrations des composants d'alliage. Pour fixer les idées,
nous avons choisi deux éléments d'alliage, Si et Mn, le premier qui élève la résistance méacanique de l'alliage et le second qui la diminue.
Nous introduisons ainsi des paramètres supplémentaires dans le modèle ce qui permet une plus grande variété de comportements.
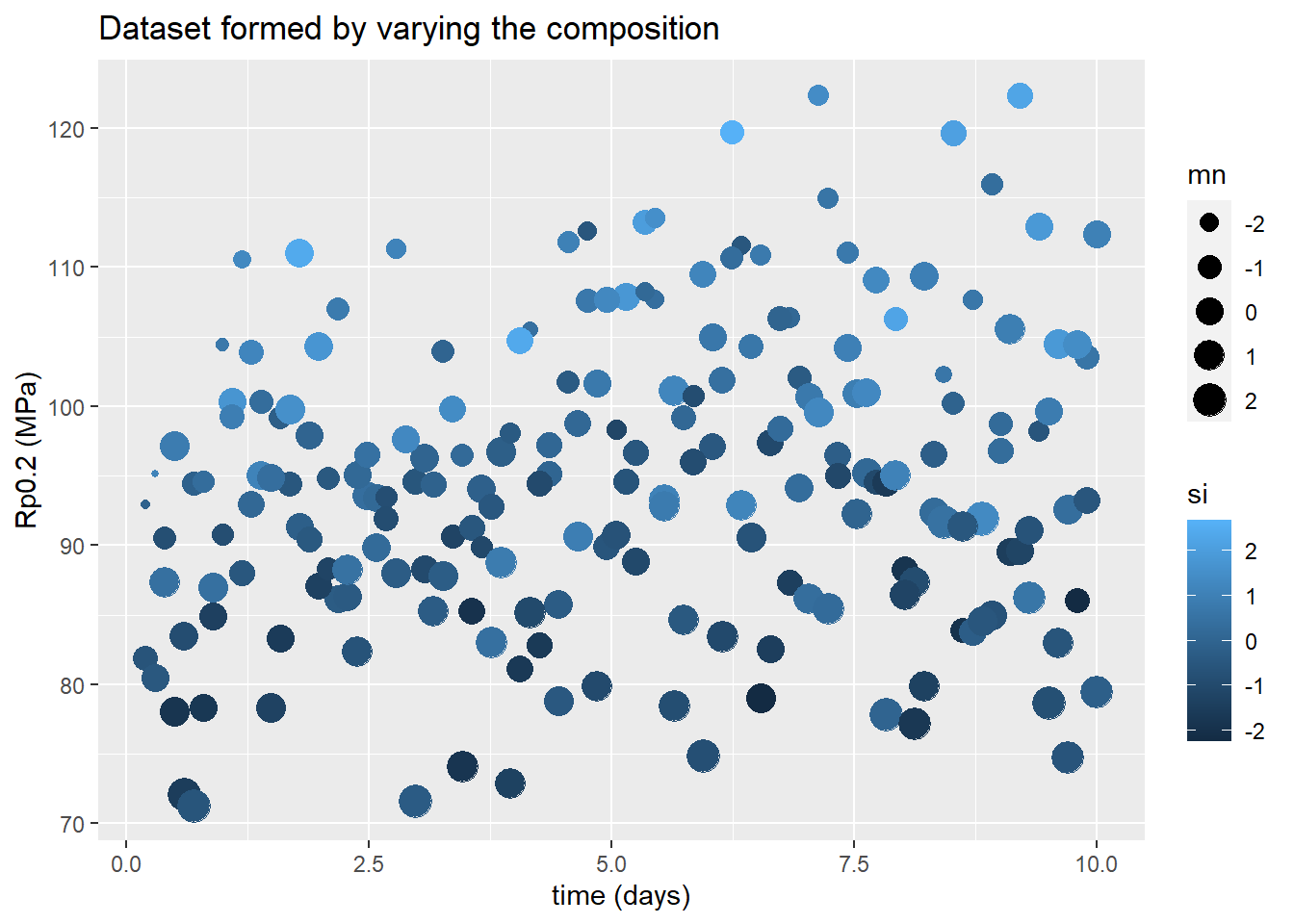
La détermination des paramètres définit ainsi un modèle qui dépend des concentrations des éléments d'alliage. L'image suivante
illustre le comportement de la courbe de vieillissement simulées dans différents cas (avec les solutions correspondantes). Si la concentration
de Si est élevée et celle de Mn est basse, on obtient la courbe verte, en haut. Si les concentrations de Si sont basse et de Mn sont hautes, on
obtient la courbe jaune, en bas. Enfin pour des concentrations semblables des deux éléments d'alliage, on obtient les courbes/zones médianes, qui montrent
que les effets sur la résistance se compensent.
