1. Oscillateur anharmonique
Introduction
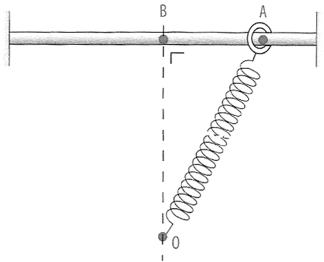
Ce projet a son origine dans une manipulation de laboratoire avec un chariot sur un rail. Le chariot est relié à un point fixe
sous le rail par un ressort. Lorsque le chariot est écarté de sa position d'équilibre (qui est en fait une zone, à cause du frottement
mécanique (frottement de Poisson), il commence à osciller en freinant. L'amplitude des oscillation décroît linéairement avec le temps.
Ce système mécanique simple se révèle donner naissance à un problème analytique assez complexe d'oscillateur anharmonique de degré 3,
obtenu en développant l'équation du mouvement de façon polyômiale (évidemment le degré 3 est arbitraire. L'objectif initial était d'analyser
les corrections à apporter au terme linéaire pour exprimer qualitativement la solution numérique.
Historiquement, en 1923 lorsque Werner Heisenberg tenta de découvrir les lois de la mécanique quantique, il s'intéressa exactement à ce problème.
Par la suite, comme ce problème fait intervenir des termes pairs et impairs, il opta pour un système sans le terme de degré 2 (cf. Jagdish Mehra,
The Historical Developpment of Quantum Theory), qu'il traita par un développement en série de Fourier. Ce nouveau
problème l'amena à découvrir les relations de commutation qui portent désormais son nom et qui forment le fondement de la mécanique quantique.
Dans le problème qui nous occupe, l'équation fondamentale s'écrit
$$
\frac{d^2}{dt^2}x=-\omega_0\left(1-\frac{\ell_0}{\sqrt{d^2+x^2}}\right)\,(x+\mu\, d\, \mathrm{sign}(\frac{d}{dt} x))
$$
Cette équation du mouvement est développées au degré 3 dans l'expression
$$
\frac{d^2}{dt^2}z=-\omega_0^2 z+\alpha z^2 -\beta z^3
$$
où \(\omega_0^2=\frac km\), \(d=OA\) et \(\ell_0\) est la longueur du ressort au repos et \(z=\frac xd\).
Le terme en \(z^2\) est celui qui rompt la symétrie de parité et qu'Heisenberg a supprimé dans sa quête de la mécanique quantique.
Solution
Le nombre d'oscillation pour un écart initial \(z_0\) est exprimé par $$ n=\frac {z_0}{4\mu} $$
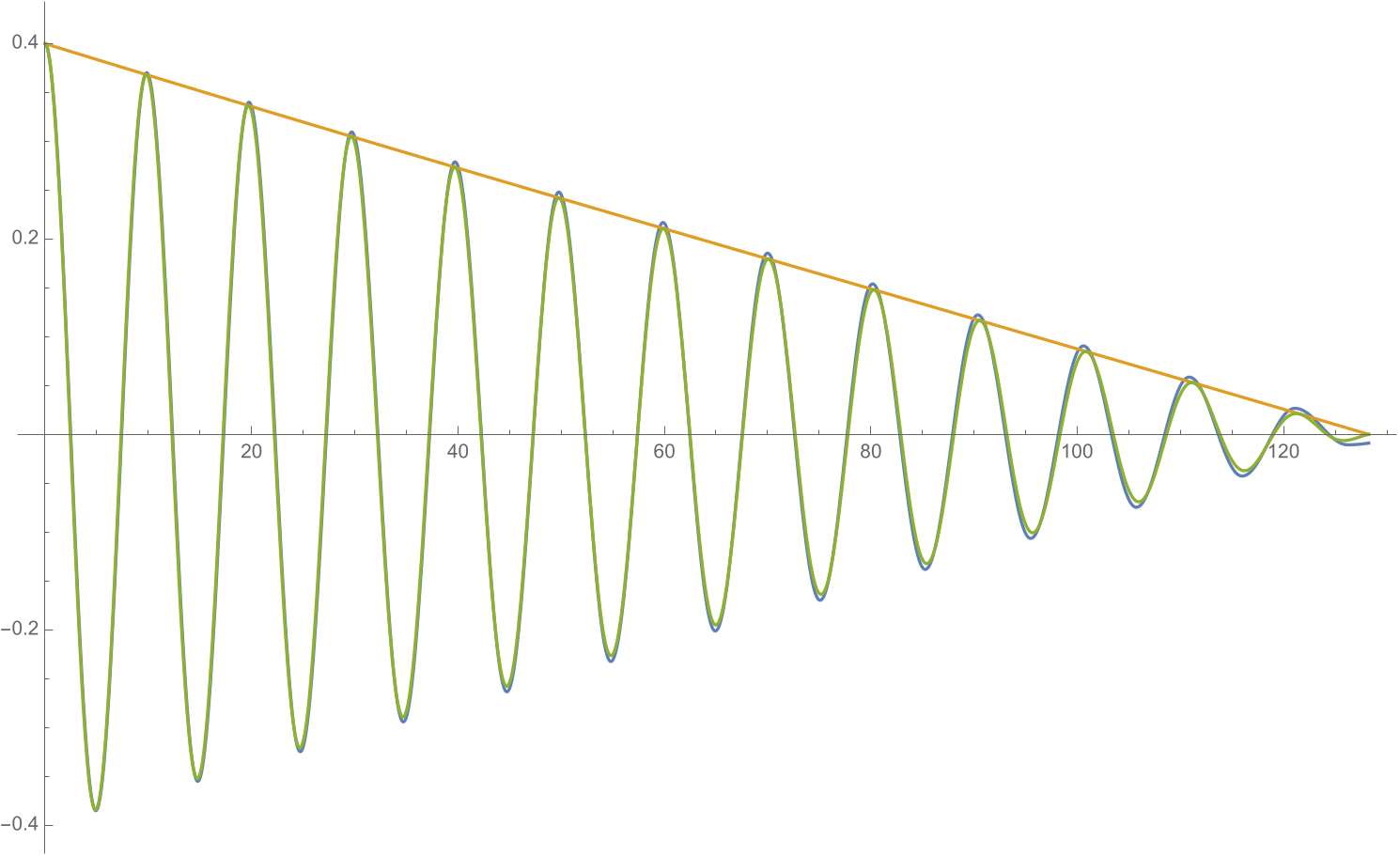
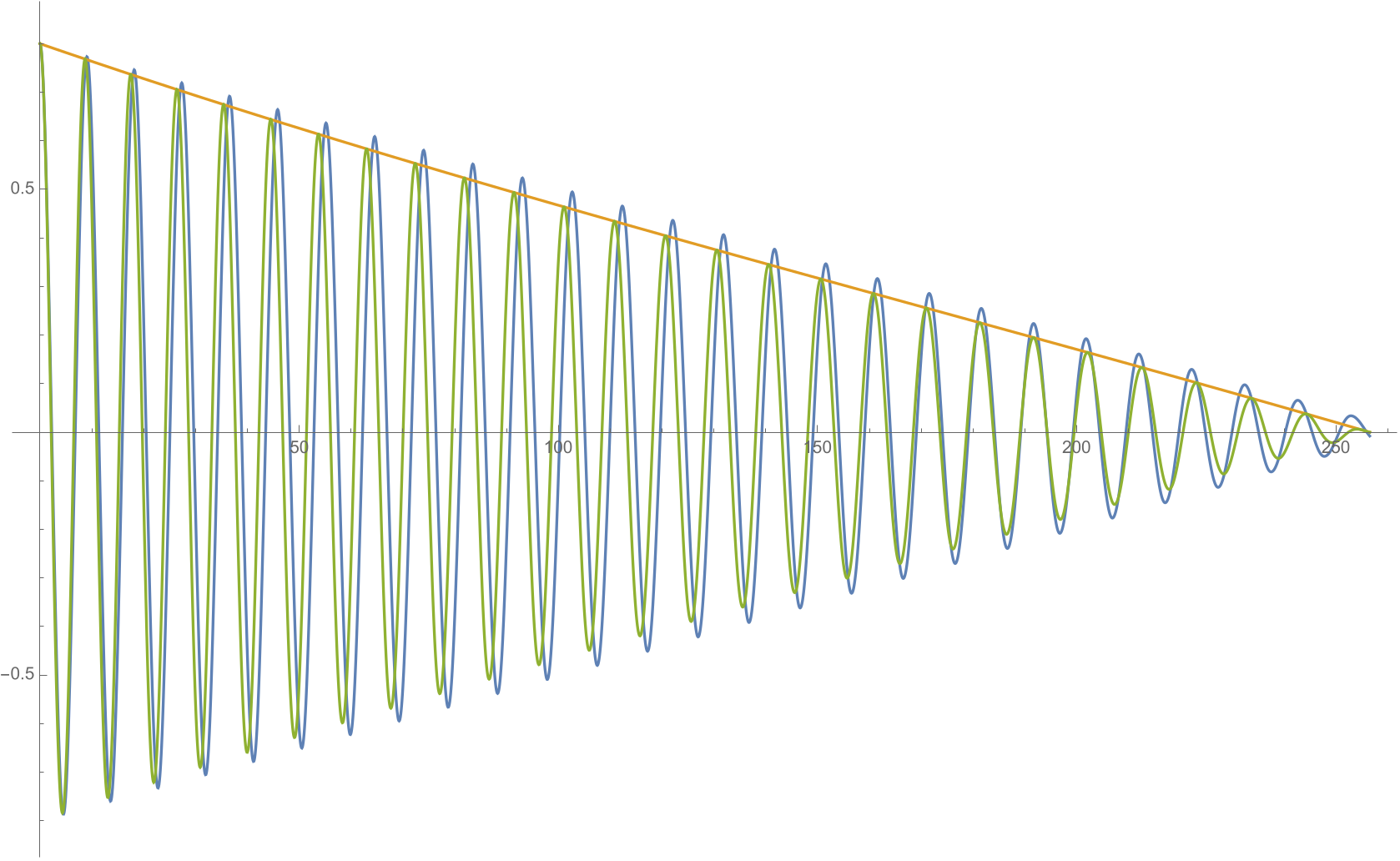
Les graphes suivants comparent la solution numérique complète (en bleu) avec la solution ne contenant les termes du développement à l'ordre 3 (en vert). Le graphe de gauche concerne les petites amplitudes initiales \(z_0=0.4\) et le graphe de droite les amplitudes plus grande \(z_0=0.8\).